Знаете ли за настройката на ESP32 ADC?: 29 стъпки

2024 Автор: John Day | [email protected]. Последно модифициран: 2024-01-30 07:52

Днес ще говоря за по-технически проблем, но мисля, че всеки, който работи с ESP32, трябва да знае: проблемът с ADC (аналогово-цифров преобразувател) за четене. Намирам това за важно, защото когато правите "измерване", особено с инструмент, който има аналогов изход, трябва да сте абсолютно сигурни, че отчитането се извършва правилно.

Във видеото днес ще извършим измервания, използвайки „аналогово-цифровия преобразувател“на ESP32, ще наблюдаваме несъответствията в преобразуването и ще приложим метод за настройка / калибриране на ADC.

Стъпка 1: Какво представлява AD Converter?

AD преобразувател е схема, способна да преобразува аналогово (непрекъснато) количество в цифрови (дискретни) стойности. Какво означава това? Това означава, че докато цифровите стойности могат да приемат само дискретни стойности, образувани от комбинацията от нули и единици, аналоговото количество може да приеме всяка стойност в рамките на диапазон. Например, ако измерваме напрежението на идеална AA клетка, бихме могли да намерим всяка стойност между 0V и 1.5V, тъй като това е аналогово количество. Изходното състояние на идеалната лампа трябва да приема само две състояния (изключено или включено), което е дискретна величина. Тъй като микроконтролерите работят по тази дискретна логика, се нуждаем от схема, способна да преобразува аналогово количество в цифрово (или дискретно).

Стъпка 2: Използвани ресурси

• Една карта Lolin32 Lite v1.0.0

• Осцилоскоп Tektronix TDS1001C за улавяне

• Един USB кабел за ESP32

• Осцилоскоп Hantek DSO4102C като генератор на сигнал

Стъпка 3: ESP32 ADC

Според данните на Espressif, чиповете ESP32 могат да представят +/- 6% разлика от един чип към друг в измерените резултати.

Освен това преобразуването НЯМА линеен отговор за всеки наличен диапазон за четене. Espressif предоставя метод за калибриране и предлага на потребителите да прилагат други методи, ако считат за необходимо да се постигне желаната точност.

Ще извършим събиране на данни и от това ще покажем отговорите на ADC и пример за прилагане на математически процес за четене на корекцията.

Има няколко (по -прости или по -сложни) начини за извършване на тези поправки. От вас зависи да оцените най -подходящия за вашия проект.

Този, показан тук, ще има илюстративна цел и ще се опита да отговори на интересни моменти, които могат да бъдат наблюдавани по време на корекциите.

Стъпка 4: Използвана верига

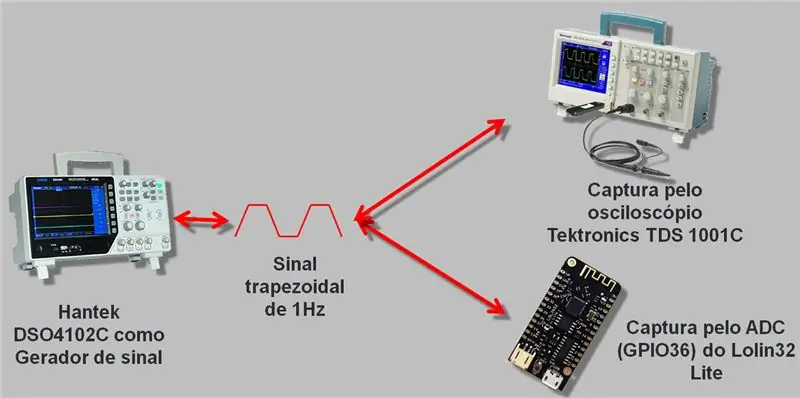
Използвах осцилоскоп с генератор на сигнали, който достига до 25 MHz, Hantek DSO4102C. Ние генерирахме вълна, която беше разчетена от ESP A / D и осцилоскопа. Събраните данни бяха записани в csv и в електронна таблица, която ще оставя в края на статията за изтегляне.

Стъпка 5: Използвайте знак

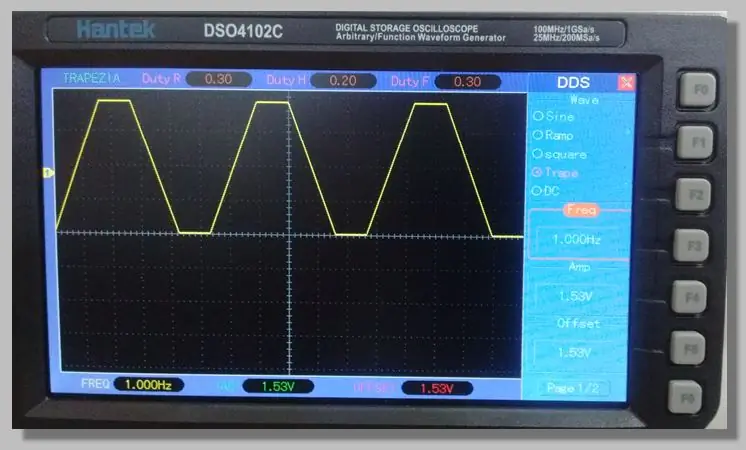
Избрахме нискочестотен трапецовиден сигнал, който позволява достъп до рампите, които преминават през целия обхват на преобразуване. Това позволява голям брой проби на тези рампи.

Стъпка 6: Данни, получени от осцилоскопа

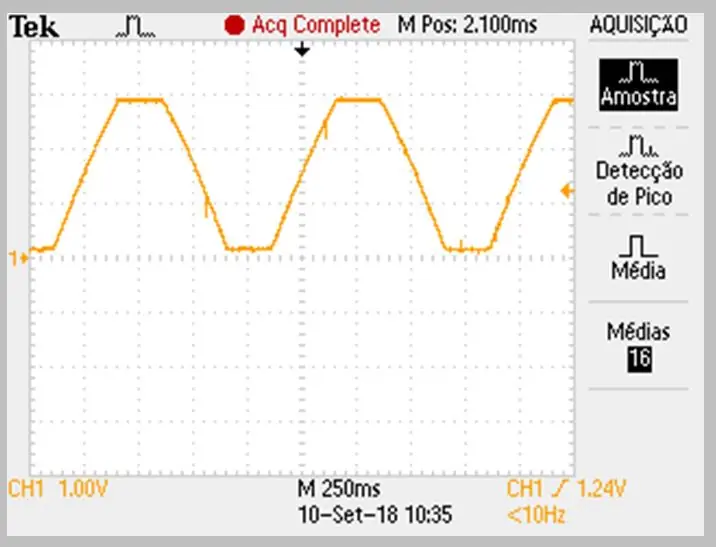
Изображението на заснемането е извършено от осцилоскопа. Данните се съхраняват в csv файл. Обърнете внимание на лекото изкривяване на нарастващите и падащите рампи на сигнала.

Стъпка 7: Данни, получени от осцилоскопа (csv файл в Excel)

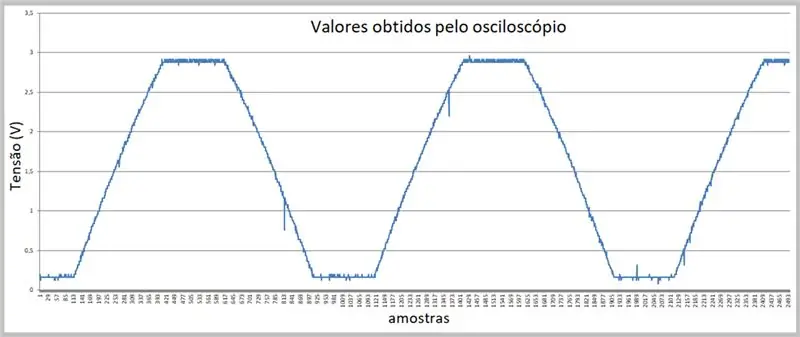
Тук имаме пробите.

Стъпка 8: Данни, получени от ADC

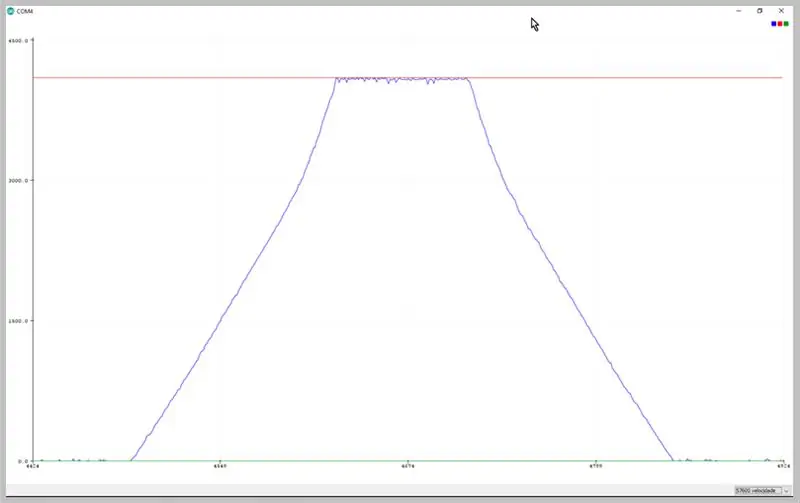
Чрез промяна на скоростта на предаване на сериала, можем да видим данните, уловени от ADC. Наблюдавайте деформацията на трапецовидния сигнал.

Данни, наблюдавани на серийния плотер на Arduino IDE

Стъпка 9: Данни, получени от ADC - Excel

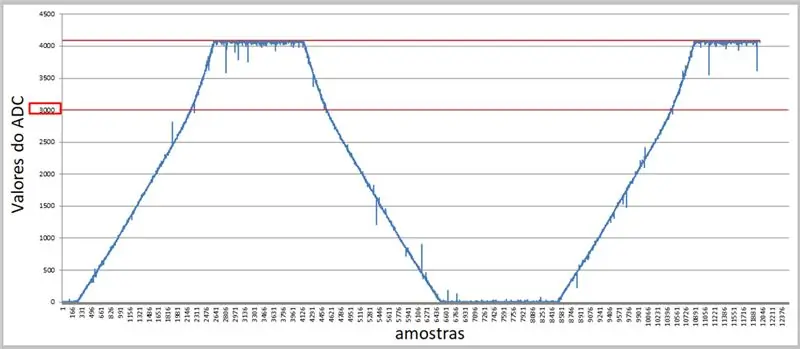
Използвайки по -висока скорост и сериен терминал, можем да уловим стойностите и да ги приложим в Excel за нашите сравнения.

Стъпка 10: Сравнение на рампи за изкачване

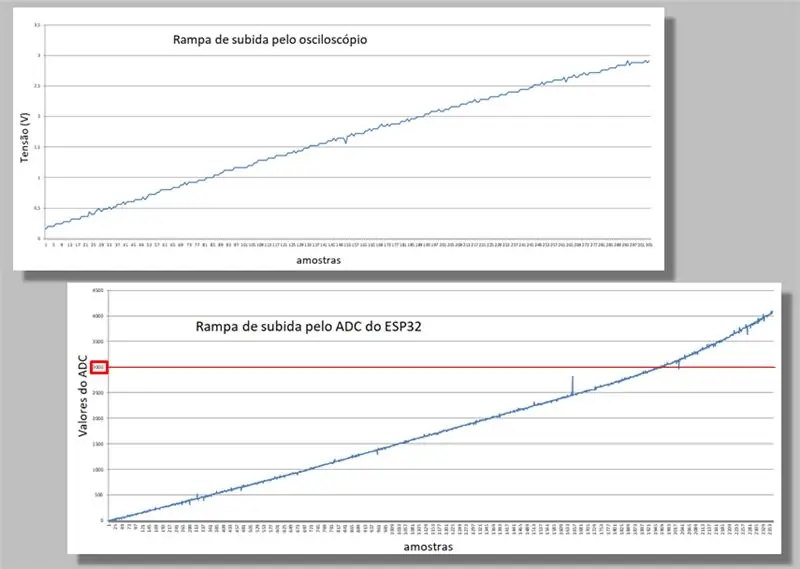
Сравняваме двете катерачни рампи на двата улова.

Обърнете внимание на кривината, която възниква на двете рампи.

Обърнете внимание също, че за една и съща рампа имаме много повече проби от ESP32, отколкото от осцилоскопа.

Стъпка 11: Приравняване на броя на пробите

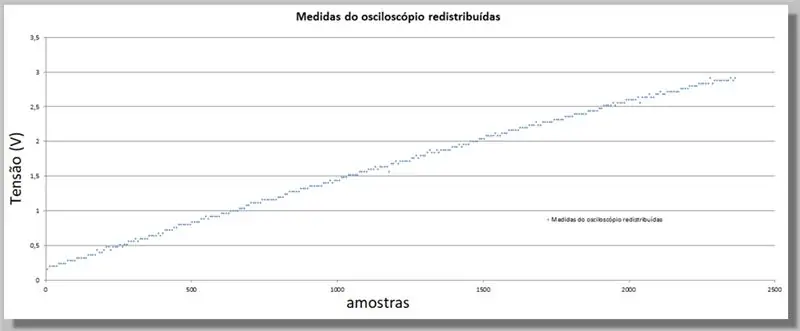
Тъй като ESP32 предоставя по -голям брой проби от осцилоскопа, трябва да приравним тези стойности, тъй като те ще служат като индекс за сравнение на двете криви.

За това ще направим директно сравнение.

Имаме 305 проби за осцилоскопната рампа и 2365 проби за ADC рампата.

Тъй като рампите са от същия обхват, можем да кажем, че имаме приблизително 7,75 проби от ADC за всеки осцилоскоп.

Умножаването на индекса на всяка проба от осцилоскоп има същата крива, но с индекси, еквивалентни на ADC и преразпределените данни.

За да попълним липсващите данни за новите позиции, ще приложим крива, която статистически отговаря на известните данни.

Стъпка 12: Попълване на пропуските - линия на тенденция

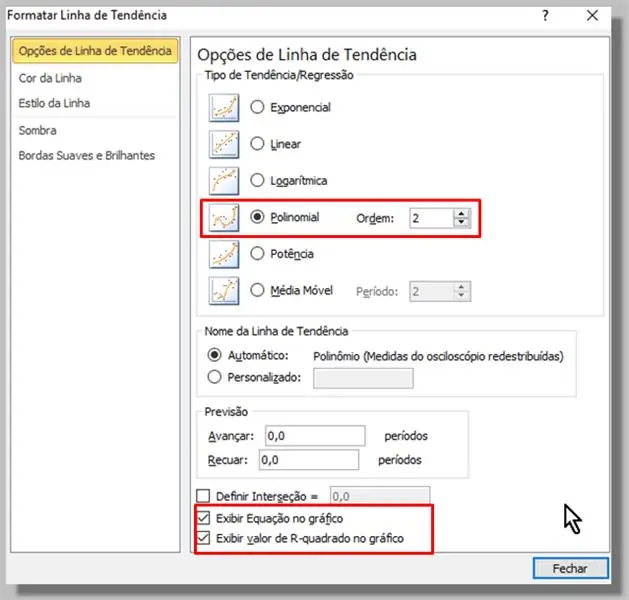
Избирайки известните данни (сини точки), като щракнете и след това щракнете с десния бутон, избираме: „Добавяне на линия на тенденция …“

В прозореца, който се показва, избираме типа полином (ред 2 ще бъде достатъчен).

Проверихме и опциите „Преглед на уравнението в диаграмата“и „Показване на R-квадратна стойност в диаграмата“.

Кликваме върху „Затвори“.

Стъпка 13: Попълване на празнините - полиномиална крива от степен 2

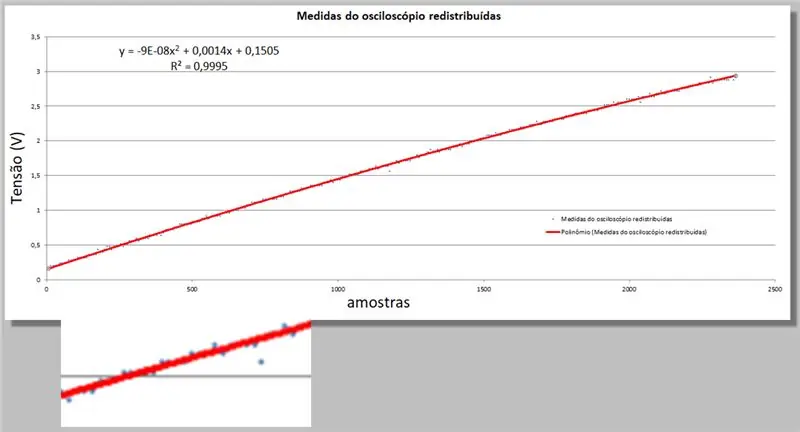
Excel ни дава две нови части информация; уравнението от втори ред, което най-добре отговаря на данните, и уравнението с R-квадрат, което определя количествено тази адекватност.

Само не забравяйте, че колкото по -близо до 1, толкова по -подходящо е уравнението.

Нека не се задълбочаваме в математиката, а просто да я използваме като инструмент.

Стъпка 14: Попълване на празнините - Оценка на функцията

Нека попълним пробивите в извадката с данните, генерирани от уравнението. И след това ги сравнете точка по точка.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Напрежение на осцилоскоп = -9E -08 * индекс2 + 0, 0014 * индекс + 0, 1505

Стъпка 15: Преобразуване на напрежението на осцилоскопа в еквивалентна стойност за сравнение с ADC

Нека се възползваме от това, за да трансформираме и стойността на напрежението на осцилоскопа в еквивалентна стойност на ADC.

Тъй като най -високата стойност, получена в ADP на ESP32, е 4095, което е еквивалентно на отчитането на 2.958V за същия индекс, можем да кажем, че:

Всеки волт в измерванията на осцилоскопа се равнява приблизително на 1384,4 единици от AD. Следователно можем да умножим всички измервания на осцилоскопа с тази стойност.

Стъпка 16: Сравняване на двете получени рампи

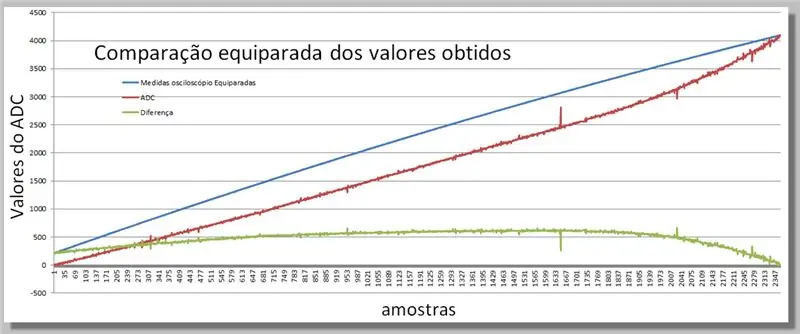
Визуализиране на разликите, получени в двете показания.

Стъпка 17: Поведение на разликата в четенето на ADC (ГРЕШКА)

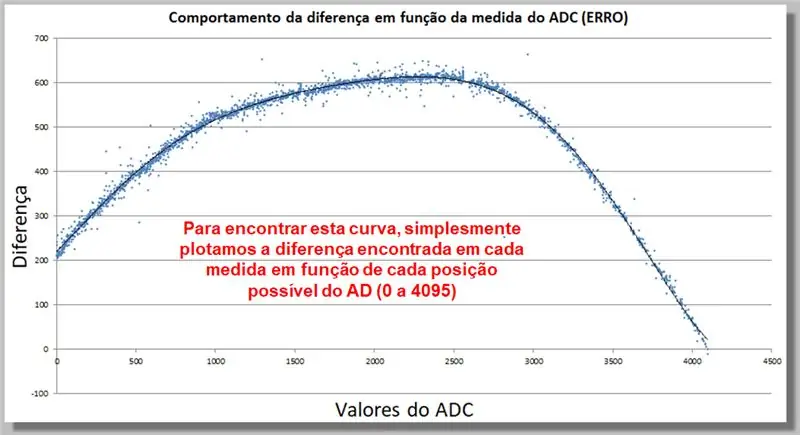
Кривата по -долу показва как разликата в показанията на ADC се държи като функция на измерването. Тази колекция от данни ще ни позволи да намерим функция за корекция.

За да намерим тази крива, просто начертаваме разликата, намерена във всяка мярка, като функция от всяка възможна позиция AD (0 до 4095).

Стъпка 18: Различно поведение при четене на ADC - Намиране на коригираща функция

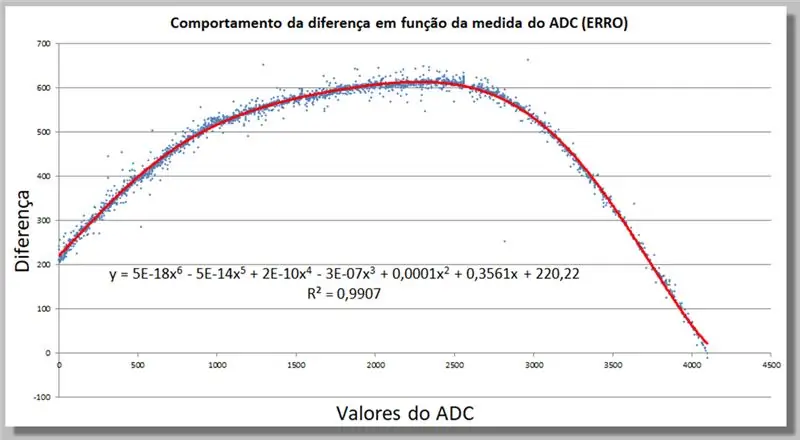
Можем да определим в Excel корекционна функция, като добавим линия на тенденция, вече с по -висока степен, докато тя съответства достатъчно на нашите данни.

Стъпка 19: Използване на друг софтуер

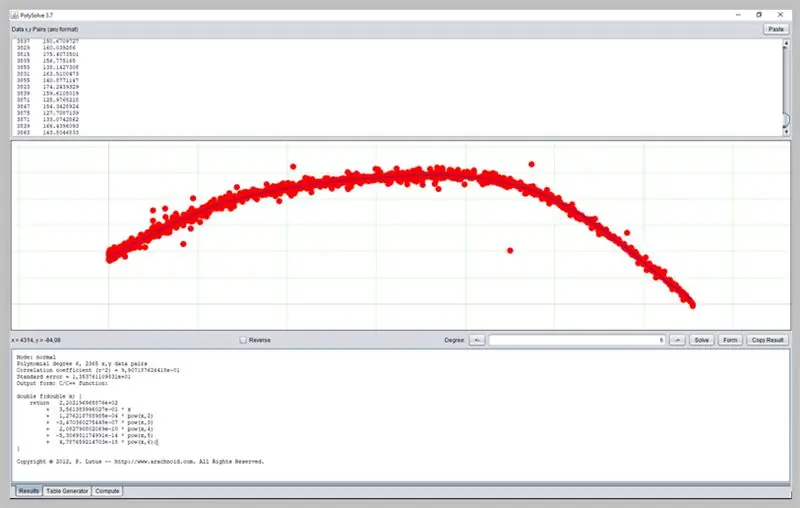
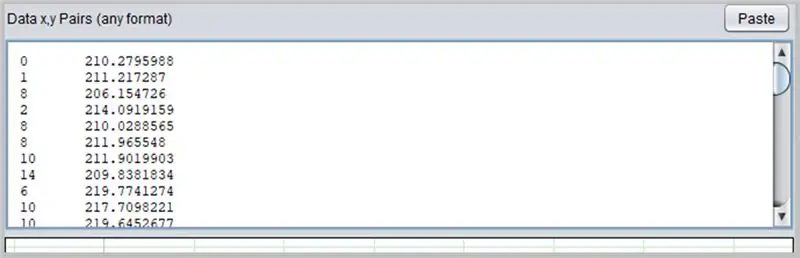
Друг интересен софтуер за определяне на криви е PolySolve, който може да се използва директно на връзката: https://arachnoid.com/polysolve/ или да се изтегли като Java приложение.

Позволява прилагането на полиномни регресии от по-висока степен и доставяне на форматираната функция, както и други функционалности.

За да го използвате, просто въведете данните в първото текстово поле. Данните трябва да следват реда X, Y, разделени със запетая или раздел. Бъдете внимателни, когато използвате точката правилно като десетична точка.

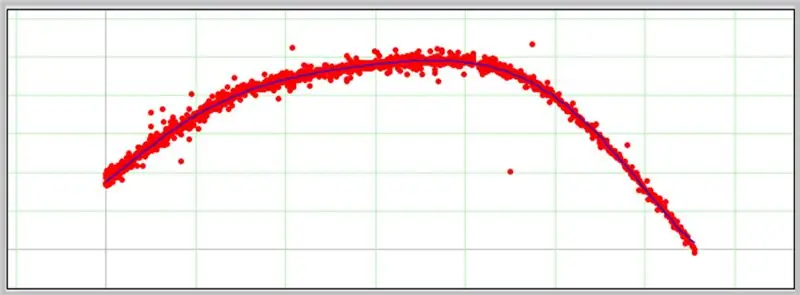
Диаграма ще се появи в следващото поле, ако въведените данни са правилно форматирани.

Ето как премина нашата крива за грешки на ADC.

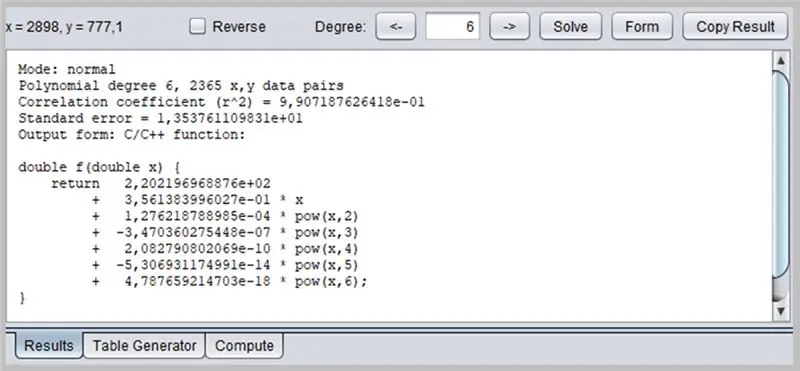
Този прозорец ще представи резултата от регресията, включително данни за адекватност на функциите, които от своя страна могат да имат форматиране на изхода си по няколко начина: като функция на C / C ++, списък с коефициенти, функция, написана на Java и т.н.

Забележка: Обърнете внимание на десетичните разделители

Стъпка 20: Константи и настройка ()

Тук посочвам GPIO, използван за аналогово улавяне. Инициализирам серийния порт, както и щифта, определен за аналогово улавяне.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Почта на сериен портален портал за отстраняване на грешки pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Стъпка 21: Loop () и коригиращата функция

Ние правим улавяне на коригираното напрежение и отпечатваме стойностите с или без правилните корекции.

void loop () {int valor_analogico = analogRead (pin_leitura); // реализиране на captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Забележете в ред 12, че имаме възможност да отпечатаме данните с добавяне на функцията за разлика f (analog_value).

Стъпка 22: Използване на функцията за корекция PolySolve

Тук използваме функцията PolySolve вътре в Arduino IDE.

/* Режим: нормален Полиномиална степен 6, 2365 x, y двойки данни Коефициент на корелация (r^2) = 9, 907187626418e-01 Стандартна грешка = 1, 353761109831e+01 Изходна форма: C/C ++ функция: Copyright © 2012, стр. Lutus - https://www.arachnoid.com. Всички права запазени. */ double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Обърнете внимание на промяната запетая като точка като десетичен разделител.

Стъпка 23: Заснемане с корекция - Плотер сериен

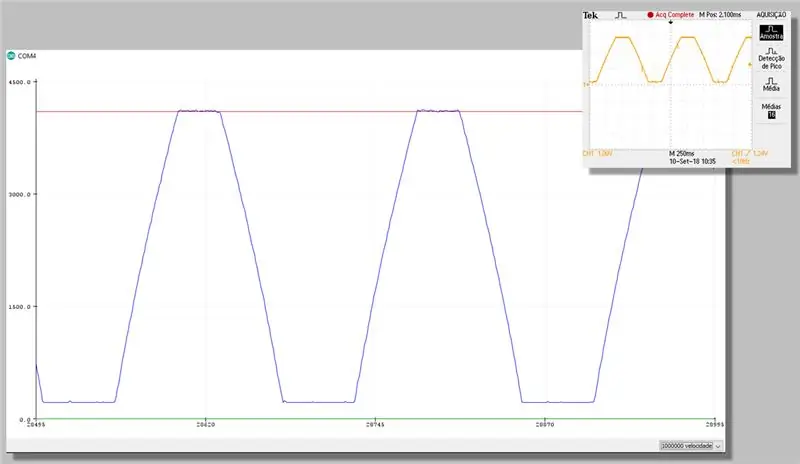
Стъпка 24: Изчислителни разходи

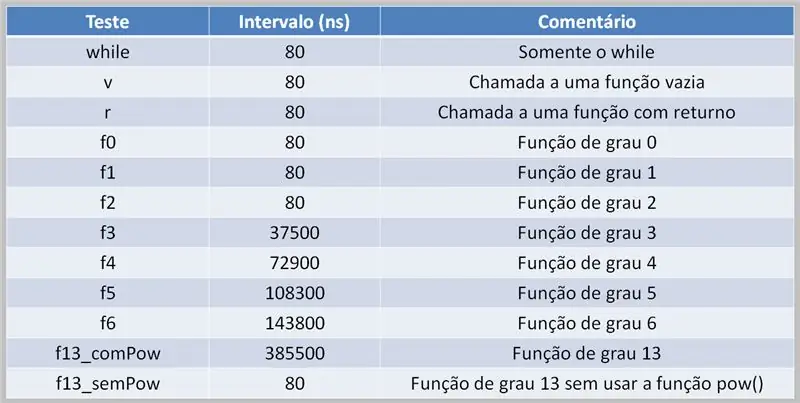
За извършване на полиномиални изчисления е необходимо процесорът да се справи с тази задача. Това може да доведе до забавяне на изпълнението, в зависимост от изходния код и наличната изчислителна мощ.

Тук виждаме таблица с резултати от тест, използващ многостепенни полиноми. Забележете разликата между времето, когато функцията pow () е била използвана, и когато не е била.

Стъпка 25: Тестов код - Настройка () и Loop Start ()

Тук имаме кода, използван в нашия тест.

void setup () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantidade de chamadas float contador = 0.0; // contador de chamadas

Стъпка 26: Тестов код - цикъл () и обработка

Използвах функцията micros (), за да получа стойността в микросекунди.

// ============= inicia o processo float agora = micros (); // marca o instante inicial while (contador <квантидада) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } агора = (микрос () - агора) / квантидада; // детерминация за intervalo que se passou para cada iteração // ============= finaliza o processo

Стъпка 27: Тестов код - Цикъл () - Резултати

Отпечатваме стойността, върната от функцията клас 13 със и без POW за сравнение, както и интервала на обработка.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM и функционален POW Serial.print (" -"); // imprime o intervalo do processamento Serial.println (agora, 6); }

Стъпка 28: Тестов код - Използвани функции

Празни функции (само с връщане) от степен 0 и 1.

// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 double f0 (double x) {return 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 double f1 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Функции от 2, 3 и 4 клас.

// FUNÇÃO DE GRAU 2double f2 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4); }

Функции от 5 и 6 клас.

// FUNÇÃO DE GRAU 5double f5 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Функция 13 клас, използваща POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Функция 13 клас без използване на POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Стъпка 29: Файлове

Изтеглете файловете:

PDF

АЗ НЕ

Електронна таблица