
- Автор John Day day@howwhatproduce.com.
- Public 2024-01-30 07:54.
- Последно модифициран 2025-01-23 14:36.

Здравейте! За да задоволя интереса си към програмирането и да се надявам да помогна на вашия, бих искал да ви покажа 3D Viewer, който кодирах в javascript. Ако искате да разширите разбирането си за 3D игри или дори да създадете своя собствена 3D игра, този прототип 3D визуализатор е идеален за вас.
Стъпка 1: Теория

За да разберете теорията на този 3D визуализатор, можете просто да проучите начина, по който гледате заобикалящата ви среда (помага да имате само един значителен източник на светлина). Забележи това:
- Обекти, които са по -далеч от вас, заемат по -малка част от вашето зрително поле.
- Обектите, които са по -далеч от източника на светлина, изглеждат по -тъмни на цвят.
- Тъй като повърхностите стават по -успоредни (по -малко перпендикулярни) на източника на светлина, те изглеждат по -тъмни на цвят.
Реших да представя зрително поле с куп линии, произтичащи от една точка (аналогично на очната ябълка). Подобно на топка с шипове, линиите трябва да бъдат равномерно раздалечени, за да се гарантира, че всяка част от зрителното поле е представена еднакво. На горната снимка забележете как линиите, идващи от шипката, се раздалечават, докато се отдалечават от центъра на топката. Това помага да се визуализира изпълнението на програмата на наблюдение 1, тъй като плътността на линиите намалява, тъй като обектите се отдалечават по -далеч от централната точка.
Линиите са основната единица на зрение в програмата и всяка от тях е нанесена на пиксел на дисплея. Когато линия пресича обект, съответният й пиксел се оцветява въз основа на разстоянието му от източника на светлина и ъгъла му от източника на светлина.
Стъпка 2: Теория за внедряване

За да се опрости програмата, източникът на светлина е същият като централната точка (очна ябълка: точка, от която се гледа картата и откъдето произтичат линиите). Аналогично на това, че държите светлина точно до лицето си, това премахва сенките и позволява яркостта на всеки пиксел да се изчисли много по -лесно.
Програмата използва и сферични координати, с централна зрителна точка в началото. Това позволява лесно да се генерират линиите (всяка с уникален тита: хоризонтален ъгъл и фи: вертикален ъгъл) и осигурява основата на изчисленията. Линиите със същия тета се съпоставят с пиксели в същия ред. Phis на съответните ъгли се увеличава във всеки ред пиксели.
За да се опрости математиката, 3D картата се състои от равнини с обща променлива (обща x, y или z), докато другите две не-общи променливи са ограничени в диапазон, завършвайки дефиницията на всяка равнина.
За да се огледате с мишката, уравненията на програмата се отчитат във вертикално и хоризонтално въртене по време на преобразуването между сферични и xyz координатни системи. Това има ефект на предварително оформяне на въртене върху набора от линии на зрението „шипова топка“.
Стъпка 3: Математика
Следните уравнения позволяват на програмата да определи кои линии пресичат всеки обект и информация за всяко пресичане. Изведох тези уравнения от основните уравнения на сферични координати и 2D уравненията на въртене:
r = разстояние, t = theta (хоризонтален ъгъл), p = phi (вертикален ъгъл), A = въртене около оста Y (вертикално завъртане), B = въртене около оста Z (хоризонтално въртене)
Kx = (sin (p)*cos (t)*cos (A)+cos (p)*sin (A))*cos (B) -sin (p)*sin (t)*sin (B)
Ky = (sin (p)*cos (t)*cos (A)+cos (p)*sin (A))*sin (B)+sin (p)*sin (t)*cos (B)
Kz = -sin (p)*cos (t)*sin (A)+cos (p)*cos (A)
x = r*Kx
y = r*Ky
z = r*Kz
r^2 = x^2+y^2+z^2
осветление = Klight/r*(Kx или Ky или Kz)
p = arccos ((x*sin (A)*cos (B)+y*sin (A)*sin (B)+z*cos (A))/r)
t = arccos ((x*cos (B)+y*sin (B) -p*sin (A)*cos (p))/(r*cos (A)*sin (p)))
Стъпка 4: Програма

Надявам се, че този прототип на 3D визуализатор ви е помогнал да разберете работата на 3D виртуалните реалности. С още по -усъвършенстване и кодиране, този зрител със сигурност има потенциала да бъде използван при разработването на 3D игри.
Препоръчано:
ESP32 COVID19 STATUS VIEWER: 4 стъпки

ESP32 COVID19 STATUS VIEWER: Този проект просто получава статус на COCID19 във формат json и го показва в OLED
Бебешки монитор Arduino с Java Viewer: 8 стъпки (със снимки)
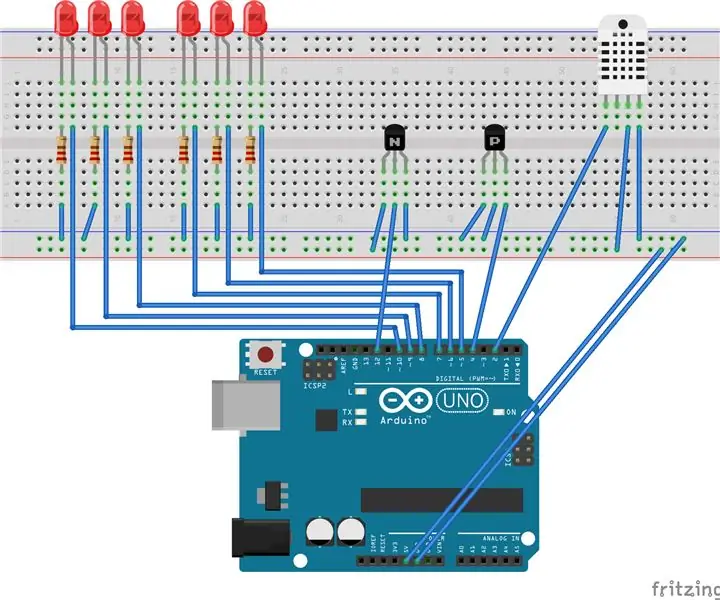
Бебешки монитор Arduino с Java Viewer: Изградете мултисензорен модул, базиран на Arduino, за да наблюдавате условията в стаята. Това устройство може да усеща влажност, температура, движение и звук. Приложен е визуализатор, базиран на java, който получава серийни данни от arduino
Headup Web Cam Viewer: 7 стъпки

Headup Web Cam Viewer: Скорошен запис разглежда търговска система, която позволява на потребителите да гледат директно на своята уеб камера, докато все още могат да видят човека, с когото говорят - стил Teleprompter - Това е моето мнение за тази идея. Лесно е да се конструира като съществено
Компютърен екран X-Ray Viewer: 4 стъпки
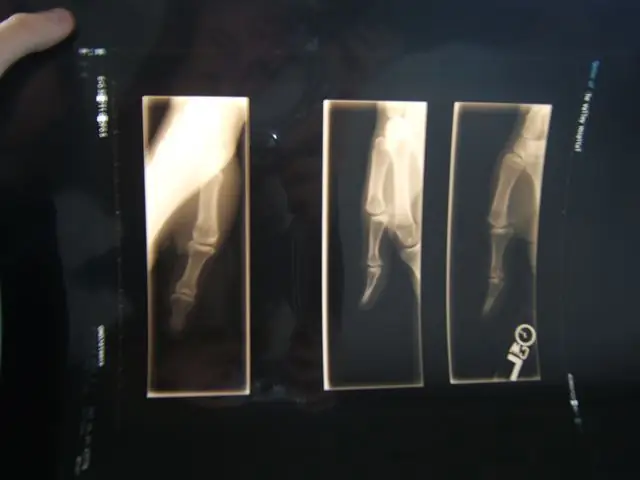
Компютърен екран X-Ray Viewer: Това е прост метод за използване на компютъра като светлинна кутия за гледане на рентгенови лъчи. Счупването на костите ви току -що достигна нови нива на забавление
Подгревател за китки на Photo Viewer: 5 стъпки

Photo Viewer Wrist Warmer: Купих си един от тези ключодържатели за преглед на снимки, той беше само десет, така че си помислих " да защо не, може да успея да го хакна в нещо готино ". то? Разглобете го и го залепете в подгревател за китки
