
Съдържание:
- Стъпка 1: Генерирайте NxN матрица от равномерни квадрати
- Стъпка 2: Рандомизиране на мрежата
- Стъпка 3: Вземете нови разстояния
- Стъпка 4: Изберете точка и сравнете разстоянието от тази точка до други
- Стъпка 5: Преместете се на нова точка
- Стъпка 6: Force = K*разстояние
- Стъпка 7: Променете движението на мрежата поради преместената точка
- Стъпка 8: Готов код
- Автор John Day day@howwhatproduce.com.
- Public 2024-01-30 07:53.
- Последно модифициран 2025-01-23 14:36.

Клетките са в състояние да взаимодействат със заобикалящата ги извънклетъчна матрица (ECM) и могат както да прилагат, така и да реагират на силите, упражнявани от ECM. За нашия проект ние симулираме взаимосвързана мрежа от влакна, които биха действали като ECM и виждаме как мрежата се променя в отговор на движението на една от точките. ECM е моделиран като взаимосвързана система от пружини, които първоначално са в равновесие с нетна сила нула. Тъй като към мрежата се прилага сила в отговор на движението на точката, ние се опитваме да накараме свързаните точки да реагират на силата по такъв начин, че да се опитат да се върнат в равновесие. Силата се следи от уравнението F = k*x, където k е пружинната константа и x е промяната в дължината на влакното. Тази симулация може да помогне да се даде общо разбиране за разпространението на сила във влакнести мрежи, което в крайна сметка може да се използва за подпомагане на симулирането на механотрансдукция.
Стъпка 1: Генерирайте NxN матрица от равномерни квадрати


За да започнем кода, избираме N, което ще определи размерите на нашата мрежа (NxN). Стойността на N може да се променя ръчно, за да се променят мрежовите размери, ако е необходимо. В този пример N = 8, така че имаме 8x8 мрежа от точки. След като генерираме матрицата, свързваме всички точки в матрицата с дължина 1 единица, като използваме формулата за разстояние, разстояние = sqrt ((x2-x1)^2+(y2-y1)^2). По този начин получаваме мрежа от квадрати, които са еднакво раздалечени от 1 единица. Това може да се види на фигура 101.
Стъпка 2: Рандомизиране на мрежата


В тази стъпка искаме да рандомизираме всички местоположения на точки с изключение на външните точки, които ще образуват нашата граница. За да направим това, първо откриваме всички координати на матрицата, които са равни на 0 или N. Тези точки са тези, които съставляват границата. За неограничените точки местоположението се рандомизира чрез добавяне на различна случайна стойност от -5 до.5 както към позициите x и y. Начертаното рандомизирано изображение може да се види на Фигура 1.
Стъпка 3: Вземете нови разстояния

След като нашата рандомизирана мрежа е създадена, ние отново намираме разстоянието между свързани точки, като използваме формулата за разстояние.
Стъпка 4: Изберете точка и сравнете разстоянието от тази точка до други



В тази стъпка можем да изберем интересна точка с помощта на курсора, както е показано на фигура 2. Не е необходимо да премествате курсора си точно върху точката, защото кодът ще я настрои до най -близката точка на свързване. За да направите това, първо изчисляваме разстоянието между всички свързани точки и точката, която току -що избрахме. След като се изчислят всички разстояния, ние избираме точката с най -малкото разстояние от избраната точка, за да стане действително избраната точка.
Стъпка 5: Преместете се на нова точка



В тази стъпка, използвайки точката, избрана в предишната стъпка, преместваме точката на ново място. Това движение се извършва чрез избиране на нова позиция с курсора, която ще замени предишната позиция. Това движение ще се използва за симулиране на упражнена сила поради промяна в дължината на пружината. На изцяло синята фигура се избира ново място. На следващата фигура движението може да се визуализира чрез оранжевите връзки, които са новите места, за разлика от сините връзки, които бяха старите места.
Стъпка 6: Force = K*разстояние

В тази стъпка прилагаме уравнението сила = k*разстояние, където k е константа 10 за колагеновите влакна. Тъй като оптичната мрежа започва в равновесно състояние, нетната сила е 0. Създаваме нулев вектор дължината на матрицата, която генерирахме по -рано, за да представим това равновесие.
Стъпка 7: Променете движението на мрежата поради преместената точка




В тази стъпка ние симулираме движението на мрежата в отговор на движението на точката, за да се върнем към нейното равновесно състояние. Започваме с намирането на новите разстояния между две точки. С това можем да намерим промяната в дължината на влакната, като разгледаме разликата между старите и новите разстояния. Можем също така да видим кои точки са се преместили, както и точките, с които са свързани, като сравняваме новите и старите местоположения на точки. Това ни позволява да видим кои точки трябва да се движат в отговор на приложената сила. Посоката на движение може да бъде разбита на нейните x и y компоненти, давайки 2D вектор на посоката. Използвайки стойността k, промяната в разстоянието и вектора на посоката, можем да изчислим вектора на силата, който може да се използва за преместване на нашите точки към равновесие. Изпълняваме този раздел от кода 100 пъти, всеки път се движим на стъпки от Force*.1. Изпълнението на кода 100 пъти ни позволява в крайна сметка отново да достигнем равновесие и като поддържаме граничните условия, виждаме промяна в мрежата, вместо просто цяла смяна. Движението на мрежата може да се види на фигура 3, като жълтото е преместените позиции, а синьото - предишните.
Стъпка 8: Готов код
Приложено в този раздел е копие на нашия код. Чувствайте се свободни да го модифицирате според вашите нужди с моделиране на различни мрежи!
Препоръчано:
Измерване на времето (часовник за измерване на лента): 5 стъпки (със снимки)

Time Measure (Tape Measure Clock): За този проект ние (Alex Fiel & Anna Lynton) взехме ежедневен измервателен инструмент и го превърнахме в часовник! Първоначалният план беше да се моторизира съществуваща рулетка. Като направихме това, решихме, че ще бъде по -лесно да създадем своя собствена черупка, с която да работим
Ултразвуков сензор за улавяне на позиционни промени на обекти: 3 стъпки

Ултразвуков сензор за улавяне на позиционни промени на обекти: Важно е ценните ви вещи да са в безопасност, би било куца, ако продължавате да пазите замъка си през целия ден. С помощта на малина pi камера можете да правите снимки в точния момент. Това ръководство ще ви помогне да заснемете видео или да направите снимката
Графиране на температурната промяна от климатичните промени в Python: 6 стъпки
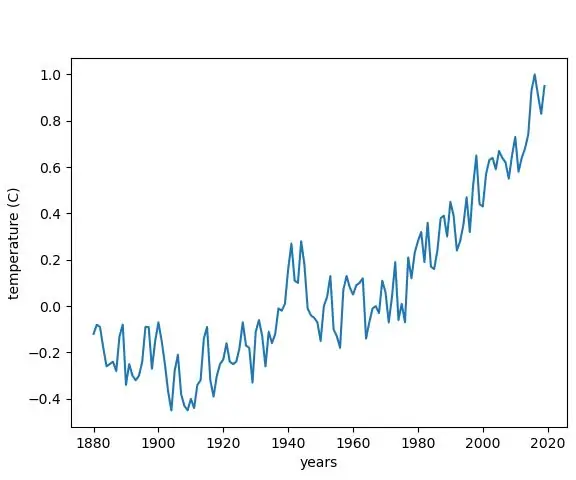
Графиране на температурната промяна от изменението на климата в Python: Изменението на климата е голям проблем. И много хора сега не знаят колко е нараснал. В тази инструкция ще начертаем температурните промени в климата, дължащи се на изменението на климата. За измама можете да видите файла python по -долу
Захранване на мобилен/мобилен телефон с външна батерия или мрежа: 3 стъпки

Захранване на мобилен/мобилен телефон с външна батерия или мрежа: Въведение. Тази идея ще работи само с телефони или таблети, ако батерията е сменяема. Спазването на полярността е важно, разбира се. Моля, внимавайте да не повредите устройството си поради небрежност. Ако не сте сигурни в способността си да направите това
Пускайте Mp3 на 70-годишен рекордер-без постоянни промени: 3 стъпки

Пускайте Mp3 на 70-годишен запис на плейър-без постоянни промени: Това, което основно направих, е да настроя моно връзка между избрания от вас MP3 или медиен източник, вашия компютър, касета, уоки-токи и директно горещо свързване към високоговорителя чрез алигаторни скоби. Както винаги, урок/демонстрационен видеоклип: МОЛЯ, ако
